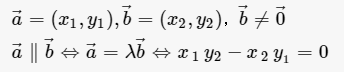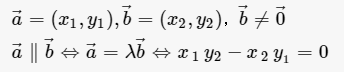若设向量a=(x1,y1),b=(x2,y2) ,向量a⊥向量b的充要条件是向量a·向量b=0,即(x1x2+y1y2)=0 。...
对于两个向量a(向量a≠向量0),向量b,当有一个实数λ,使向量b=λ向量a(记住向量是有方向的)则向量a‖向量b。反之,当向量a‖向量b时,有且只有一个实数λ,能使向量b...
向量与实数的积的坐标,等于用这个实数乘原来的向量相应的坐标。...
两个向量的数量积等于它们对应坐标的乘积的和。...
两个向量差的坐标分别等于这两个向量相应坐标的差。...
如果 b≠0,那么向量b与a共线的充要条件是:存在唯一实数λ,使得 a=λb。...
如果两个向量a.b不共线,则向量p与向量a.b共面的充要条件是存在唯一有序实数对(x.y),使p=xa+yb。...
点到直线的距离公式,即过这一点做目标直线的垂线,由这一点至垂足的距离。...
过不平行于平面的直线上一点作平面的垂线,这条垂线与平面的交点与原直线与平面的交点的连线与原直线构成的(这条线与原直线的夹角的余角)即为线面角。...