方差是衡量一个随机变量离其期望值的距离的平均值,它的定义公式为:
$$Var(X) = E[(X - E(X))^2]$$
其中,$E(X)$ 表示随机变量 $X$ 的期望值,$Var(X)$ 表示随机变量 $X$ 的方差。...
$$Var(X) = E[(X - E(X))^2]$$
其中,$E(X)$ 表示随机变量 $X$ 的期望值,$Var(X)$ 表示随机变量 $X$ 的方差。...
期望的定义公式为:$E(X)=\sum_{i=1}^n x_i p_i$,其中 $X$ 是一个随机变量,$x_i$ 是它的取值,$p_i$ 是对应的概率。在连续型随机变量的情况下,期望可以表示为 $E(X)=\int_{-\infty...
正态分布的概率密度函数公式为:
$$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
其中,$\mu$ 是正态分布的均值,$\sigma$ 是正态分布的标准差,$e$...
$$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
其中,$\mu$ 是正态分布的均值,$\sigma$ 是正态分布的标准差,$e$...
泊松分布的概率质量函数公式为:
$$P(X = k) = \frac{e^{-\lambda}\lambda^k}{k!}$$
其中,$X$ 为服从泊松分布的随机变量,$\lambda$ 为其均值和方差。...
$$P(X = k) = \frac{e^{-\lambda}\lambda^k}{k!}$$
其中,$X$ 为服从泊松分布的随机变量,$\lambda$ 为其均值和方差。...
二项分布的概率质量函数公式为:
$$P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}$$
其中,$X$ 为 $n$ 重伯努利试验中成功的次数,$p$ 为每次试验中成功的概率,$k$ 为 $X$ 取值范围内的某个...
$$P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}$$
其中,$X$ 为 $n$ 重伯努利试验中成功的次数,$p$ 为每次试验中成功的概率,$k$ 为 $X$ 取值范围内的某个...
假设$X$和$Y$是两个独立随机变量,它们的方差分别为$\sigma_X^2$和$\sigma_Y^2$,则它们的和$Z=X+Y$的方差为:
$$Var(Z) = Var(X+Y) = Var(X) + Var(Y)$$
因为$X$和$Y$是独立的,所...
$$Var(Z) = Var(X+Y) = Var(X) + Var(Y)$$
因为$X$和$Y$是独立的,所...
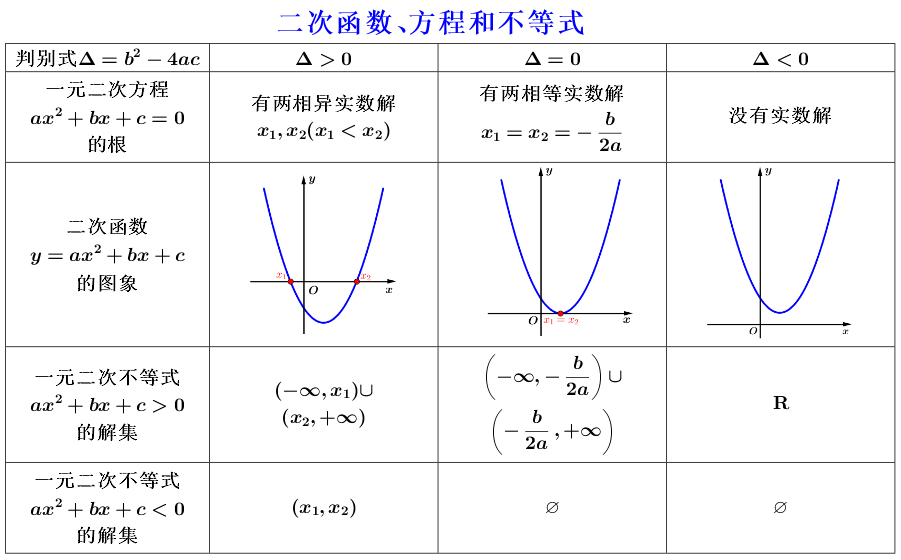
一元二次不等式是指一个形如 $ax^2+bx+c \geq 0$ 或 $ax^2+bx+c \leq 0$ 的不等式,其中 $a,b,c$ 为实数且 $a \neq 0$。我们可以通过求解一元二次方程的方法来解决这类不等式...
对于一元二次函数 $f(x) = ax^2+bx+c$,其求根公式可以通过求解方程 $ax^2+bx+c=0$ 得到。该方程的求根公式为:
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
其中,$a,b,c$ 分别为二次函...
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
其中,$a,b,c$ 分别为二次函...
标准正态分布的概率密度函数公式为:
$$f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$$
其中,$\pi$ 是圆周率,$e$ 是自然常数,$x$ 是随机变量的取值,$f(x)$ 是 $x$ 对应的概率...
$$f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$$
其中,$\pi$ 是圆周率,$e$ 是自然常数,$x$ 是随机变量的取值,$f(x)$ 是 $x$ 对应的概率...